【茨城県高校入試数学】x² − x − 12 の因数分解｜つまずきポイントを家庭教師が解説

家庭教師のセタ先生です。
今回の記事では、動画で解説した 「x² − x − 12 の因数分解」 について、
お子さんがつまずきやすいポイントを整理しながらお伝えします。

因数分解でつまずく原因は「公式を理解できていないこと」

この問題でお子さんがつまずきやすいポイントは、
因数分解の公式をきちんと理解しているかどうか です。

代表的な因数分解の公式は 4つ。
この4つは必ず覚えておかないと、この問題や類題を解くことはできません。

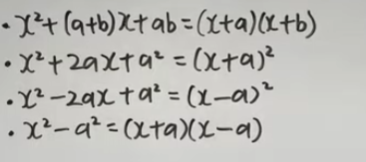
まずはお子さんに、
この4つの公式をしっかり覚えること
を最優先で徹底してください。

4つの公式のどれに当てはまるかを判断する

公式を覚えたら、次は
「この式がどの公式に当てはまるのか？」
を判断します。

x² − x − 12 は、まず最初の公式の形には当てはまりません。
この時点で、候補を 3つに絞る ことができます。

さらに、次の2つの公式は
真ん中の項が必ず 2 の倍数 になるという特徴があります。

しかし今回の真ん中の項は −1。
2の倍数ではないので、これら2つも除外されます。

つまり今回使うのは、
残った1つの公式 になります。

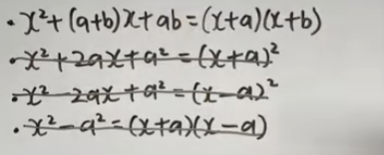
足して −1、掛けて −12 になる数字を探す

使う公式が決まったら、
次に 2つの数字の組み合わせ を考えます。

今回必要なのは、

• 足して −1
• 掛けて −12

になる2つの数字です。

この条件を満たすのは、

3 と −4

です。

実際に確認すると、

• 3 − 4 = −1
• 3 × (−4) = −12

となり、どちらも元の式の数字と一致します。

因数分解の最終形と答え

以上のことから、
x² − x − 12 を因数分解すると、

(x + 3)(x − 4)

となります。

選択肢では 「ウ」 がこの形になるので、
答えはウ です。